Bufferruimte bij inrit van parkeergarages is een ontwerpkwestie
In vakkringen hoor je er niet veel over. Een bufferruime van voldoende lengte bij een inrit van een parkeergarage is volgens ons een essentieel ontwerpelement van een parkeergarage. De NEN 2443 zegt er weinig over en geeft geen eenduidige handvatten om de lengte van een bufferruimte te berekenen. Wat staat er in de NEN 2443? Hoe is de lengte van een bufferruimte te berekenen? En tenslotte volgen een paar voorbeelden.
Van de redactie Vexpansie | Jitze Rinsma, Rinsma Parkeeradvies
Aanleiding
Doordat de grond schaarser wordt, zowel voor de bouw van garages (bufferruimte buiten het gebouw?) als voor functies in de openbare ruimte, kan er discussie ontstaan over de benodigde lengte van een bufferruimte tussen betrokkenen bij het ontwerp.
Als de bufferruimte te kort is staan bij garages wachtende auto’s op straat en leiden, die tot overlast. Ook bij de toepassing van parkeerliften x) is een bufferruimte van voldoende lengte essentieel.
De NEN 2443
Volgens de definities van de NEN 2443 (2013) is de bufferruimte van parkeergarages de ruimte voor het opstellen van personenauto’s. Dat kan zowel betrekking hebben op inrijdende auto’s als op uitrijdende auto’s.
Volgens hoofdstuk 5.2.2 van de NEN moet tussen het trottoir en de ontsluitingsweg van een openbare parkeervoorziening (bij een inrithelling van meer dan 3%) een horizontaal vlak van minimaal 5 meter aanwezig zijn. Deze eis geldt niet voor niet-openbare parkeergarages en stallingsgarages.
De toelichting op de normtekst (dat is geen normtekst!) geeft aan dat de factoren die de grootte van de bufferruimte bepalen zijn:
– de verkeersituatie op de weg,
– het aantal in- en uitritten,
– de capaciteit van de parkeerapparatuur en
– de omvang van het autoverkeer dat de garage binnenrijdt.
De wachtende auto’s mogen de afwikkeling buiten de garage niet verstoren. Voor de berekening van de bufferruimte wordt in de toelichting aangegeven dat een bufferruimte van 1% à 2% van het aantal personenauto’s, dat in een maatgevend uur de garage inrijdt, voldoende is. Wel zal in situaties waarin personenauto’s gelijktijdig aankomen, een grotere bufferruimte nodig zijn. Voor verdere indicaties voor een voorontwerp wordt verwezen naar de tabellen B1 en B2 van bijlage B. Hierop wordt in dit artikel niet verder ingegaan xx).
- Het ontwerp van de inrit. Bij een rechtstand van voldoende lengte is de capaciteit hoger dan bij een inrit met bochten direct voor de parkeerapparatuur;
- Het toegangscontrole systeem en het fabricaat van het systeem. Soms wordt met zenders de toegang op afstand geopend. In het andere geval dient men te stoppen bij een inrijstation en daar een kaart aan te bieden of te trekken. Het ene fabricaat/ systeem werkt sneller dan het andere. En ook het ene snel vouwhek of roldeur werkt sneller dan het andere.
- Het in(- en uit)rijden met kwalitatief betere apparatuur, denk met name aan kentekenherkenning en optimale opstelling van terminals en camera’s, kan veel vlotter gaan als de maatvoering ervan hierop aangepast is. Wat betekent, dat de bufferruimte minder aangesproken wordt. In de NEN 2443 staat er niets over.
De wachttijd theorie
Om de lengte van de wachtrij bij een inrit van een parkeergarage te berekenen, worden de principes uit de wachtrijtheorie gebruikt. Dat betekent dat men ervan uitgaat dat de voertuigen onafhankelijk van elkaar aankomen bij een garage of terrein. De aankomstintervallen zijn negatief exponentieel verdeeld.
Gegevens die voor een berekening nodig zijn zijn:
1. λ (lambda) = Aankomstsnelheid (bijvoorbeeld auto’s per minuut)
2. μ (mu) = Servicesnelheid (hoeveel auto’s per minuut kunnen inrijden)
3. Servers (s) = Aantal inrijpoorten (of toegangen)
Rekenvoorbeelden
1. Wachttijd bij garage met een inrit en een snelle slagboom
Uitgaande van een capaciteit van 360 auto’s per uur wordt de kans op een wachtrij met meer dan 4 auto’s en het gemiddelde aantal wachtende auto’s berekend.
Als er 360 auto’s per uur door een inrit verwerkt kunnen worden, dan is μ = 360 en zijn de aankomstintervallen negatief exponentieel verdeeld.
λ Is het aantal auto’s dat per uur aankomt. De verwerkingstijd van de auto’s is negatief exponentieel verdeeld. Dat is het meest aannemelijk. Niet iedereen pakt namelijk even snel een kaartje. Evenzo varieert de benodigde tijd nodig om de geopende slagboom of roldeur te passeren.
ρ = λ/μ. De waarde ρ moet kleiner zijn dan 1, want anders zal de wachtrij voor de garage oneindig lang worden.
Wanneer er 200 auto’s in een maatgevend uur aankomen, is de waarde voor ρ = 200/360 = 0,56.
De kans dat er meer dan k auto’s in de rij staan wordt berekend met de volgende formule:
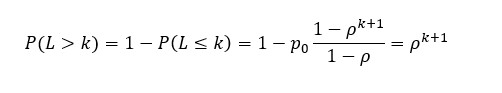
Invullen voor bijv. k = 4 geeft = 0,0550731 (afgerond 0,055 of 5,6%). Lees dit als: er is een kans van 5,6 procent op een wachtrij van 4 auto’s tijdens een maatgevend uur met een inrijdende intensiteit van 200 per uur.
Het gemiddelde aantal auto’s dat staat te wachten is:
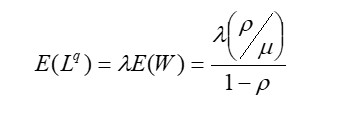
Invullen levert 200*(0.56/360)/(1-0.56) = 0,72 auto’s. Ofwel gemiddeld staat in bovengenoemde situatie nooit meer dan 1 auto te wachten. Op basis van deze uitkomsten kan de discussie gevoerd worden of deze situatie acceptabel is en hoe lang de opstelruimte moet zijn.
Met bovenstaande formules is ook voor andere situaties de gemiddelde lengte van de wachtrij en de kans daarbij op een aantal wachtende auto’s te bepalen. Uiteraard zijn de uitkomsten anders als er sprake is van oncomfortabele inrij-situaties. Die situaties kunnen ontstaan bij één of meer van – bijvoorbeeld – de volgende problemen: veel voetgangers verhinderen het vlot inrijden, verstoring door nabijgelegen verkeerlichteninstallaties, veelvuldige storingen aan het parkeersysteem of vragen om informatie via de intercom bij de inrit.
2. De wachttijd bij een garage met 1 autolift
De kans op een wachtrij met meer dan 1 auto bij de inrit kan als volgt berekend worden:
Aangenomen wordt dat er 60 auto’s per uur per inrit verwerkt kunnen worden, μ is dan 60 en negatief exponentieel verdeeld. λ is het aantal auto’s dat per uur aankomt. De verwerkingstijd van de auto’s is ook negatief exponentieel verdeeld. Dat is het meest logisch, aangezien niet iedereen even snel een kaartje pakt en evenveel tijd nodig heeft om een rit te maken.
ρ = λ/μ en moet kleiner zijn dan 1 (anders zal de wachtrij oneindig lang worden). Wanneer er 20 auto’s per uur aankomen, is de ρ = 20/60 = 0,33.
De kans dat er meer dan k auto’s in de rij staan:
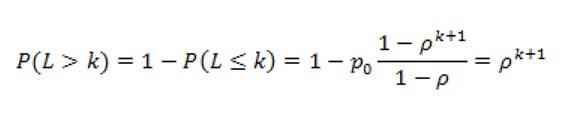
Invullen voor k = 2, ρ = 0,33² = 0,1089. Het bovenstaande toegepast op verschillend aantal in en uitrijders per uur laat het volgende zien:
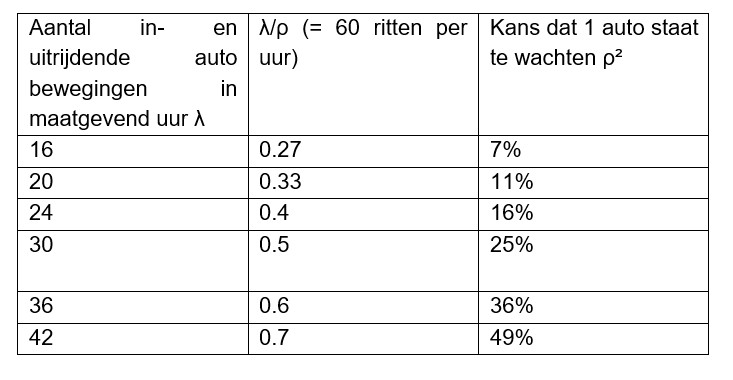
Er is van uitgegaan dat de servicetijd voor in- en uitrijden gelijk is.
Uit bovenstaande benadering blijkt dat bij een (totale) rit tijd van 60 seconden al dat bij relatief geringe aantallen de autolift in- en uitrijdende auto’s sprake zal zijn van wachten van auto’s. Zo zal, als er 20 auto’s in een uur in- of uit willen rijden, 11% moeten wachten.
Afsluitend
De ruimte in stedelijke gebieden is schaars en zal de komende jaren nog schaarser worden. Bij realisatie van garages moet de bufferruimte bij de inrit niet het kind van de rekening worden. Een bufferruimte van voldoende lengte is belangrijk. Ten behoeve van het ontwerp kan zoals aangegeven deze berekend worden met de locatie specifieke gegevens van o.a. het aantal inrijdende auto’s in een maatgevend uur en de afhandelingstijd van toegangscontrole apparatuur.
En zoals eerder aangegeven is een keuze van goede apparatuur, detaillering van de inrit en van de locatie van de apparatuur (terminals, camera’s, detectielussen, slagbomen, snelvouw hekken) essentieel voor een zo groot mogelijke capaciteit van de inrit.
Een proefopstelling na het maken van het detailontwerp kan bij twijfel helpen voor het realiseren van een optimale situatie.
Nadien kan de berekende lengte in het ontwerp worden opgenomen.
NEN 2443 2013 blz. 112 Figuur B1
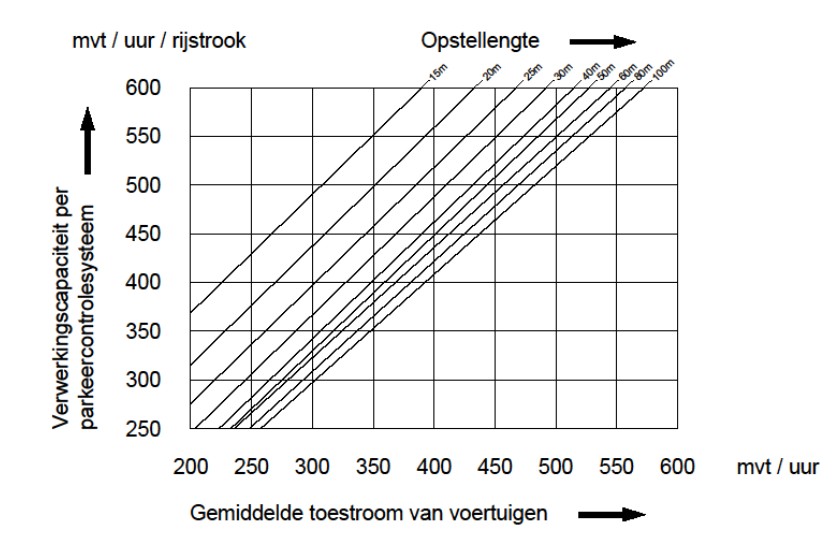
x) kleine garages < 20 pp en garages met parkeerliften vallen niet onder het toepassingsgebied van de NEN 2443
xx) Ter aanvulling het volgende: In de vorige NEN 2443 gepubliceerd in 2000 wordt in de toelichting aangegeven dat figuur B.1 (identiek aan die in de NEN uit 2013) is overgenomen uit de Zwitserse en Duitse ontwerpvoorschriften. Op internet zijn deze genoemde ontwerpvoorschriften niet (meer) aangetroffen. Figuur B1 is hierboven opgenomen
Bekijk meer artikelen
VvE's bang voor elektrische auto in garage
Media berichten dat verenigingen van eigenaren (VvE’s) elektrische auto’s soms weigeren in de garages onder hun appartementencomplex uit toenemende vrees voor brand
Lees meerStacker parking systems in relatie tot brandveiligheid
Wat zijn de verrassende oplossingen van Stacker Parking Systems in relatie tot brandveiligheid? Daarover vertelde Sven Sterkendries tijdens de Vexpan online lunchbijeenkomst
Lees meerEffect groener Nederland op brandveiligheid parkeergarages
Om het Klimaatakkoord te behalen, dat in 2019 werd gepresenteerd, moet Nederland een reductie van broeikasgasemissies aantonen. Er worden verschillende maatregelen getroffen
Lees meerBrandrisico van open parkeergarages
Voor parkeren in de buitenlucht, op parkeerterreinen, zijn geen brandveiligheidsvoorzieningen aan de orde. Er is geen sprake van een bouwwerk
Lees meerTips: bescherming tegen cyberaanval parkeergarages
Bijna dagelijks komt in het nieuws dat grote bedrijven worden gehackt. Ook parkeergarages kunnen te maken krijgen met cybercriminaliteit. Ethisch hacker
Lees meerInfographic Veilig parkeren en laden elektrische voertuigen
Er komen steeds meer elektrisch aangedreven auto’s in Nederland. Om veilig parkeren en laden van deze voertuigen in parkeergarages mogelijk te maken is een infographic opgesteld
Lees meer